Intuitive explanation of Conditional Probability and Bayes theorem

Conditional probability

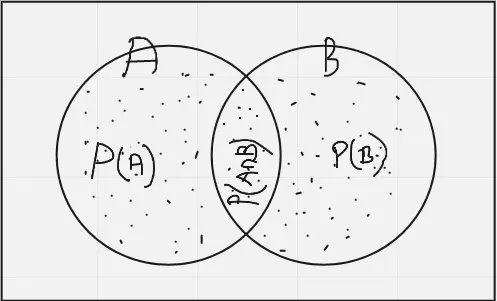
So what does the equation P(A|B)=P(AnB)/P(A) tryinh to tell? consider venn-diagram chart as shown in the figure, We are trying to intuitively understand what P(A|B) means. P(A|B) ask a question “What is the probability of occurence of event A given that Event B has already occured?”. Now lets focus on the chart,imagine the let us imagine that i choosed one dot at random and i realized that the dot is from region covered by circle B, now what is the probability that the same dot lies inside the region covered by circle A? or in other words what is P(A|B)? lets suppose that the area cover by the region that lies in the intersection of the region A and B is 20 percent of the total region covered by circle B, then we can easily say that P(A|B)=0.2(i.e 20 %).

for example: in the above figure Region AEFGrepresents area covered by small rectange and region ABCD represnets area covered by big rectangle then if i am choosing the dot at random, the probability that the dot lies is region inside small rectangle is given by (Area of small rectangle AEFG)/(Area of big rectangle ABCD) assuming dots are uniformly distributed inside these region.

Now how do we compute what portion of the region A is covered by the intersecting region between region A and B? Yeah, we can calculate this by (Area of intersecting region)/(Area of region A).This is exactly how P(B|A)=P(AnB)/P(A) is derived.

Bayes Theorem

Now we are in the condition to get feeling for the equation P(B|A)=P(AnB)/P(A) and P(A|B)=P(AnB)/P(B) by thinking about them in terms of area

from above two equations we can easily derive that P(A|B)=P(B|A)*P(A)/P(B)

Now to intuitively understand this bayes therem there is nothing much to understand since we already understood conditional probability. just think about numerator as the area of the intersecting region beteween regions A and B and dividing by P(B) is just asking what portion of the B’s region is covered by the intersection region between region A and B.

important takeaways

P(A|B) represents what portion of the B’s region is covered by intersection region betwenn region A and B

so P(A|B)*P(B) translates to Area of the intersecting region

and hence P(B|A)=P(A|B)*P(B)/P(A) gives the portion of A’s region covered by the intersecting region because numerator gives the area of intersection region.