Attention is all you need (Oversimplified)

What things we don’t need?

The transformer was introduced in the paper “Attention is all you need”. Before transformer architecture was introduced, the best-performing models also connect the encoder and decoder through an attention mechanism, This paper proposed a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely. Hence by “Attention is all you need” it is referring that we don’t need complex RNN and CNN in a network to make a good language model.

Problem with the recurrence-based model.

The best-performing model before the attention mechanism and mainly two problems, we take an example of an encoder-decoder network with attention. First is the sequential processing of the data, due to the use of recurrence each token was processed sequentially failing to parallelize, which increased the training time of the model. Another problem was the word embeddings. Consider the word “Bat” it can have two meanings depending on the context “He hit the ball with the bat” and “Bat is the mammal”. “Bat” refers to two different things in these two sentences. but in the previous model, using pre-trained embedding or using an embedding layer to learn the word embedding these two “Bat” have the same embedding vector. This is undesirable. The problem to this problem is introduced in the transformer model, in this model we use a self-attention mechanism to produce better contextual embedding for each word.

Types of attention used in transformers architecture

Attention was introduced before the transformer was introduced, transformer model only replaced the use RNN with self-attention. While talking about the transformers we should remember that there are two variants of the attention used in the transformer’s architecture, self-attention, and encoder-decoder-attention. There are two self-attention one each in the encoder and decoder side and one encoder-decoder-attention block that is present in the decoder side of the network but attends to the outputs of the encoder side.

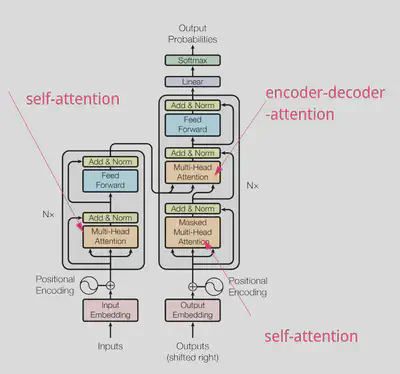
Why use self-attention?

We can think of self-attention as a technique for obtaining more contextualized word embedding, that not only depends on global context but also depends on the current context, It is very much similar to word2vec and Glove in terms of what it helps to obtain. just imagine that we already have word2vec embeddings, using self-attention we can improve on this embedding giving them the values that depend on the context of the current context of embedding. Hence the best way of understanding self-attention is to think of it as a way to get better word embeddings

In the above example, The word “Bat” has different word embedding, which of course is what we want because they mean completely different things. Attention not only gives different word embedding for the same word in a different context it overall improves the embedding for all the words in a sentence. so self-attention is the black box that gives better word embedding when we pass sentences to it.

Self-attention calculation

First, we need to understand what thing we are trying to generate by doing self-attention calculations. in one sentence, the self-attention of a single word in a sentence is the weighted sum of the value vector of all the words in a sentence weighted by attention score. And what is attention score? The attention score of a word with another word represents how similar the query vector of the first word is to the key vector of the second word.

Calculating self-attention of a single word

Let’s look at the simplistic version of self-attention calculation first where we don’t use any of the key, query, and value vectors.

The figure above shows the self-attention calculation for the word ”Bat” in the sentence “Bat is a mammal”. To calculate the similarity score the embedding vector of the “Bat” is compared with the embedding vector of all the words. This gives the attention score of that word for all the other words in a sentence, which can be then used to weigh the embedding vector to calculate the final self-attention vector. We can think of the similarity score as a dot product score though in real applications scaled dot product version is used. But in the above isn’t the dot product between “Bat” with itself always 1? yes but for this example, I have knowingly made that mistake to explain the weighted sum.

Actually

1. We don’t calculate the score using similar exact word embeddings

   What we do is linearly transform the word embeddings to get a transformed vector called keys. Again pass the word embedding to another linear transformation to obtain the vector called queries. if we want to calculate the attention score for the word “Bat” we calculate the scaled dot product of the query vector of the word with a key vector of the rest of the words. The result is then passed to the softmax to get the probability score.

2. We don’t calculate the weighted sum of the exact word embeddings.

   What we do is linearly transform word embeddings to get the new set of vectors called values and then weight these values vectors instead using the attention score calculated in the previous step

Hence, in conclusion, we pass the word embedding through three Linear layers to get key, query, and value vectors, and then

$Attention Score=Softmax(Dot(Queries(“Bat”),Keys))/\sqrt{D_k})$

$Selfattention=WeightedSum(AttentionScore,Values)$

The calculation of the self-attention value for the single word of the sentence is shown in the figure below. While calculating the attention values for all the words in a sentence the computation is made faster using Matrix calculations.

Calculation of self-attention for a single word

Calculating self-attention of a complete sentence

If Q represents the 2-dimensional matrix which contains a query vector for each word, K represents the 2-dimensional matrix which contains a key vector for each word and V represents the 2-dimensional matrix which contains a Value vector for each word. Then self-attention of all the words in a sentence can be calculated using the matrix operation shown below.

$$ SelfAttention(Q,K,V)=Softmax(\dfrac{QK^T}{\sqrt{d_k}})V $$

What is multiheaded attention?

In the transformer model, we use multi-head attention. It’s a very simple concept. We calculate self-attention multiple times and concatenate the result. For example, if we want the multiheaded attention with a number of heads equal to 8, then we will generate 8 triplets of the Q, K, and V matrix. And then calculate self-attention 8 times, At the end, the result is concatenated so the multiheaded attention value of a single word is 8 times the length of simple attention. Multiheaded attention help captures multiple relations that are present in the sentence. This improves the performance of the transformer significantly.

Figure showing multiheaded attention with 3 heads, K, Q, V is calculated 3 times using a different linear transformation.

A simple analogy

We can think of multiheaded attention this way, Suppose we want the dumb machine to differentiate two cubes, we show them a bunch of examples and tell it to learn the relation. Initially, we initialize the parameter randomly and after showing a bunch of examples, let’s say the dumb machine learned the relation that it can compare cubes by comparing the sizes, The interesting fact is that that are multiple ways that cubes can be compared, if we start the training all over again it may learn the to compare cube by different relation lets say by “weight”, each time we run the training it may learn different relation between cubes, this is because we start from the randomly initializes state. A multiheaded version of this would use multiple weights to learn different relationships in a single training run and combine the result so that we can differentiate the cube better based on multiple properties

The problem created by discarding RNN and positional embedding.

Transformers do not use a sequential model like RNN, Immediate disadvantage might hit our mind “But RNN provided Order in the sequence” when we process the sequence sequentially, there was order information inbuilt. But since the transformer is a highly parallelizable model we need some way to solve the problem related to the position. There must be something that the model can use to differentiate the order of the tokens in the sequence. Let,s say we have the word embedding size of $d_{model}$ then for each word it’s positional encoding also will be the vector of the same dimension. Which is then added element-wise to the embedding before feeding it into the self-attention layer. Positional encoding is the function of the token’s position in the sequence and is calculated using the following equations. These two equations’ representation represents the calculation of positional encoding for tokens at odd and even positions.

$$ PE_{pos,2i}=sin(pos/1000^{2i/d_{model}} $$

$$ PE_{pos,2i+1}=cos(pos/1000^{2i/d_{model}} $$

Masked self-attention

Consider the language translation task, where our training dataset has pair of sentences in two different languages, we feed the sentence of one language on the encoder side and then get the sentence of the other language on the decoder side, we use self-attention both in encoder and decoder. We should not forget that on the decoder side we generate the output word one at a time, so while calculating the self-attention on the decoder side we should not allow the model to attend to the words that are in the future. if we are trying to predict the fourth word in a sequence we should only allow the model to the attention to the three tokens that come before the fourth token. For this, we use masking, which helps us discard attending to the future tokens from the output sequence.

Summary

1. Each word in a sentence is passed to the self-attention layer parallelly and then to the feed-forward layer, To retain the positional information, positional encoding is calculated and added element-wise to each word embedding.
2. Multi-headed self-attention is used to learn multiple relationships
3. Masked self-attention is used on the decoder side to only attend to the past words/tokens.
4. Encoder-Decoder attention used in the transformer’s architecture is the same as the encoder-decoder attention used in the seq-to-seq model described in the previous post.